Lies, Damned Lies, and Statistics
-
Hah...fair enough, though I'm now curious as to how you ended up at 8 in 10...but if everyone else can can wait for the answer, I suppose I can wait for the explanation.
-
Since you guys did so well on that one, here's another: I hand you a bag, inside which are three coins. The coins appear identical, but while two are "fair," one will always land heads-up.
You pull a coin from the bag, and toss it three times. You get a head every time. What are the chances you pulled the unfair coin?
(Those who get this right might be ready for the extremely unintuitive Monte Hall problem...)
@mzimmers said in Lies, Damned Lies, and Statistics:
JonB nailed it. His analysis was spot-on, with one minor nit: The problem stated:
Someone devises a test for this disorder which, in correctly diagnoses all cases, but also reports a false positive exactly 1% of the time. As stated, the false positive rate is given without regard to any true positives -- it occurs at a rate of 1%. In a population, it will "lie" about 10 individuals.
So you meant "1% of the whole population receives a false positive" (
P(B ∩ ¬A) = 0.01).I thought you meant "1% of the healthy people receive a false positive" (
P(B | ¬A) = 0.01).@JonB said in Lies, Damned Lies, and Statistics:
P(A | B) = P(A ∩ B) / P(B) = 0.001 / 0.01099 so P(A | B) = 0.0909918... which is a teensy bit more than 1 in 11.
There is still something wrong here with where you go about calculating these figures, but I'm too tired to spot it.
It boiled down to the interpretation of the false-positive rate (see above). With the correct interpretation, we have:
P(A) = 0.001(0.1% of the population have the disorder)P(B | A) = 1(The test detects the disorder 100% of the time)P(B ∩ ¬A) = 0.01(The test has a 1% false positive rate within the whole population)
Finding intermediate parameters,
- P(B∩A) = P(B|A) * P(A) ⇒
P(B ∩ A) = 0.001(0.1% of the whole population have the disorder AND get a positive result) - P(B) = P(B∩A) + P(B ∩ ¬A) ⇒
P(B) = 0.011(1.1% of the whole population get a positive test result)
Finally,
- P(A | B) = P(A∩B) / P(B) ⇒
P(A | B) = 1/11(Given that I got a positive result, I have 1 in 11 chance of having the disorder)
All good! :-D
@mzimmers said in Lies, Damned Lies, and Statistics:
Since you guys did so well on that one, here's another: I hand you a bag, inside which are three coins. The coins appear identical, but while two are "fair," one will always land heads-up.
You pull a coin from the bag, and toss it three times. You get a head every time. What are the chances you pulled the unfair coin?
I used the same method as my first attempt. Same equations, just different starting numbers.
P(X|Y) = 0.8where- X: Got the unfair coin
- Y: Flipped 3 times and got 3 heads
P.S. Thanks for the fun puzzles, @mzimmers! I used to do them in school/university but haven't done any in a while.
-
Hah...fair enough, though I'm now curious as to how you ended up at 8 in 10...but if everyone else can can wait for the answer, I suppose I can wait for the explanation.
I don't use @JKSH 's equations --- too much brainache!
The method is just:
- There are 8 permutations from flipping a coin 3 times.
- The unfair coin produces 3 heads in all of its permutations.
- The fair coins each produce 1 set of 3 heads in each of theirs.
- Thus of the possible 24 outcomes, there are 10 with all heads, and of those 2 are produced by the fair coins while 8 are produced by the weighted one.
Hence my initial writing of
8 in 10, rather than simplifying :)You should probably now throw Monte Hall at @JKSH :)
-
Well done, and well presented. When I was faced with this problem, I did it slightly differently (1/3 * 100%) vs. (2/3 * 12.5%). The underlying logic is the same.
JKSH's notations are just a formal representation of what we're doing. Given that I took my only statistics class nearly 40 years ago, I've forgotten all the notation, though I remember most of the principles. As long as we all get to the right answers, the various approaches are equally valid.
I'll bring up Monte Hall if KJSH chimes in. And yes, I can remember watching that show live...good entertainment (if you're 12 years old).
-
Well done, and well presented. When I was faced with this problem, I did it slightly differently (1/3 * 100%) vs. (2/3 * 12.5%). The underlying logic is the same.
JKSH's notations are just a formal representation of what we're doing. Given that I took my only statistics class nearly 40 years ago, I've forgotten all the notation, though I remember most of the principles. As long as we all get to the right answers, the various approaches are equally valid.
I'll bring up Monte Hall if KJSH chimes in. And yes, I can remember watching that show live...good entertainment (if you're 12 years old).
Given that I took my only statistics class nearly 40 years ago, I've forgotten all the notation, though I remember most of the principles
In that case, please remind me what the "Chi squared" test thingy is? I remember the teacher banging on about that one. And no, you are not allowed to look it up. :)
-
Chi squared...ew.
"Math's hard; let's go shopping!" (Barbie from the pre men-are-pigs era)
-
I don't use @JKSH 's equations --- too much brainache!
The method is just:
- There are 8 permutations from flipping a coin 3 times.
- The unfair coin produces 3 heads in all of its permutations.
- The fair coins each produce 1 set of 3 heads in each of theirs.
- Thus of the possible 24 outcomes, there are 10 with all heads, and of those 2 are produced by the fair coins while 8 are produced by the weighted one.
Hence my initial writing of
8 in 10, rather than simplifying :)You should probably now throw Monte Hall at @JKSH :)
@JonB said in Lies, Damned Lies, and Statistics:
I don't use @JKSH 's equations --- too much brainache!
I do find verbal descriptions more meaningful and intuitive, but I also find equations more systematic and comprehensive.
Descriptions help me to understand the "reality" of a problem, while equations help me to see connections and patterns (either within the same problem, or across different problems)
@JonB I've taken the liberty of translating English into Equations :-) (Your statements in bold)
- X: Got the unfair coin
- Y: Flipped 3 times and got 3 heads
Starting info:
P(X) = 1/3(I have a 1 in 3 chance of getting the unfair coin)P(Y | X) = 1(The unfair coin produces 3 heads in all of its permutations / Given that I got the unfair coin, I'm guaranteed to flip 3 heads in a row)P(Y | ¬X) = 1/8(There are 8 permutations from flipping a coin 3 times. The fair coins each produce 1 set of 3 heads in each of theirs. / Given that I didn't get the unfair coin, I have a 1 in 2^3 chance of flipping 3 heads in a row)
Intermediate parameters:
- P(¬X) = 1 - P(X) ⇒
P(¬X) = 2/3(I have a 2 in 3 chance of getting a fair coin) - P(Y ∩ X) = P(Y|X) * P(X) ⇒
P(Y ∩ X) = 1/3(I have a 1 in 3 chance of getting the unfair coin AND flipping 3 heads in a row) - P(Y ∩ ¬X) = P(Y|¬X) * P(¬X) ⇒
P(Y ∩ ¬X) = 1/12(I have a 1 in 12 chance of getting a fair coin AND flipping 3 heads in a row) - P(Y) = P(Y|X) + P(Y|¬X) ⇒
P(Y) = 5/12(of the possible 24 outcomes, there are 10 with all heads)
Finally:
- P(X | Y) = P(X ∩ Y) / P(Y) ⇒
P(X | Y) = 4/5(...[of these 10,] 8 are produced by the weighted [coin]. / Given that I flipped 3 heads in a row, there is a 4 in 5 chance that I have the unfair coin)
You should probably now throw Monte Hall at @JKSH :)
Sorry, I looked up the Wikipedia article when it was first mentioned here!
@JonB said in Lies, Damned Lies, and Statistics:
In that case, please remind me what the "Chi squared" test thingy is? I remember the teacher banging on about that one. And no, you are not allowed to look it up. :)
I don't remember how to use it anymore, but I remember using it lots in biology class to test for mutations in a population.
@mzimmers said in Lies, Damned Lies, and Statistics:
"Math's hard; let's go shopping!" (Barbie from the pre men-are-pigs era)
For me, shopping is hard. Too many choices; need to guard against marketers' tactics; need to research to find a good deal; need to haggle or negotiate...
...let's do math! It's just me, my comfy chair, and my trusty pen+paper.
-
Given that I took my only statistics class nearly 40 years ago, I've forgotten all the notation, though I remember most of the principles
In that case, please remind me what the "Chi squared" test thingy is? I remember the teacher banging on about that one. And no, you are not allowed to look it up. :)
@JonB said in Lies, Damned Lies, and Statistics:
In that case, please remind me what the "Chi squared" test thingy is?
You pose a hypothesis (e.g you have a model of something) and you want to test how well your model fits the experimental data you have - you calculate the χ squared and you get your answer. There's a lot of theory behind it, but you can think of it in simple terms as the (quadratic) measure of the population's dispersion around your model - i.e. how far the real population is from the modelled population.
-
@JonB said in Lies, Damned Lies, and Statistics:
I don't use @JKSH 's equations --- too much brainache!
I do find verbal descriptions more meaningful and intuitive, but I also find equations more systematic and comprehensive.
Descriptions help me to understand the "reality" of a problem, while equations help me to see connections and patterns (either within the same problem, or across different problems)
@JonB I've taken the liberty of translating English into Equations :-) (Your statements in bold)
- X: Got the unfair coin
- Y: Flipped 3 times and got 3 heads
Starting info:
P(X) = 1/3(I have a 1 in 3 chance of getting the unfair coin)P(Y | X) = 1(The unfair coin produces 3 heads in all of its permutations / Given that I got the unfair coin, I'm guaranteed to flip 3 heads in a row)P(Y | ¬X) = 1/8(There are 8 permutations from flipping a coin 3 times. The fair coins each produce 1 set of 3 heads in each of theirs. / Given that I didn't get the unfair coin, I have a 1 in 2^3 chance of flipping 3 heads in a row)
Intermediate parameters:
- P(¬X) = 1 - P(X) ⇒
P(¬X) = 2/3(I have a 2 in 3 chance of getting a fair coin) - P(Y ∩ X) = P(Y|X) * P(X) ⇒
P(Y ∩ X) = 1/3(I have a 1 in 3 chance of getting the unfair coin AND flipping 3 heads in a row) - P(Y ∩ ¬X) = P(Y|¬X) * P(¬X) ⇒
P(Y ∩ ¬X) = 1/12(I have a 1 in 12 chance of getting a fair coin AND flipping 3 heads in a row) - P(Y) = P(Y|X) + P(Y|¬X) ⇒
P(Y) = 5/12(of the possible 24 outcomes, there are 10 with all heads)
Finally:
- P(X | Y) = P(X ∩ Y) / P(Y) ⇒
P(X | Y) = 4/5(...[of these 10,] 8 are produced by the weighted [coin]. / Given that I flipped 3 heads in a row, there is a 4 in 5 chance that I have the unfair coin)
You should probably now throw Monte Hall at @JKSH :)
Sorry, I looked up the Wikipedia article when it was first mentioned here!
@JonB said in Lies, Damned Lies, and Statistics:
In that case, please remind me what the "Chi squared" test thingy is? I remember the teacher banging on about that one. And no, you are not allowed to look it up. :)
I don't remember how to use it anymore, but I remember using it lots in biology class to test for mutations in a population.
@mzimmers said in Lies, Damned Lies, and Statistics:
"Math's hard; let's go shopping!" (Barbie from the pre men-are-pigs era)
For me, shopping is hard. Too many choices; need to guard against marketers' tactics; need to research to find a good deal; need to haggle or negotiate...
...let's do math! It's just me, my comfy chair, and my trusty pen+paper.
@JKSH said in Lies, Damned Lies, and Statistics:
@mzimmers said in Lies, Damned Lies, and Statistics:
"Math's hard; let's go shopping!" (Barbie from the pre men-are-pigs era)
For me, shopping is hard. Too many choices; need to guard against marketers' tactics; need to research to find a good deal; need to haggle or negotiate...
In that case, you don't seem to have a woman. If you did, I would expect her to insist on making all the shopping choices on your behalf, so it wouldn't be an issue... ;-)
["JB: Unreconstructed from the pre-PC era."] -
@JonB said in Lies, Damned Lies, and Statistics:
In that case, please remind me what the "Chi squared" test thingy is?
You pose a hypothesis (e.g you have a model of something) and you want to test how well your model fits the experimental data you have - you calculate the χ squared and you get your answer. There's a lot of theory behind it, but you can think of it in simple terms as the (quadratic) measure of the population's dispersion around your model - i.e. how far the real population is from the modelled population.
-
So that's a rather different thing from standard deviation, right. So you make a model, calculate with it, then discover how inaccurate it is by going back and examining the real population, and then make something squared out of it. Is that it?
-
Bonus point for finding the χ key on your keyboard.
While I'm at it.... The other thing I remember the teach banging on about forever was to do with (unlike you I haven't a clue/the will to go find symbols to type) "x-bar" [
xwith a horizontal bar on top of it] versus "mu" [the Greek letter]. x-bar was the mean you got from a sample, while mu was the actual mean, which you didn't know.Now, the problem was something about how you had to phrase what you said about x-bar & mu in your conclusion. I presume this was to do with confidence limits, you were trying to say something like "I'm 95% sure x-bar is within one standard deviation of mu". Only there was some deep rule you had to adhere to in phrasing it some way round with some wording. Like, you couldn't say x-bar or mu was likely to be whatever, because it wasn't subject to probability (perhaps that was for mu, because the mean of the population just is whatever it is, even if you don't what that is, or some-such). So what was that one all about? :)
-
-
-
So that's a rather different thing from standard deviation, right. So you make a model, calculate with it, then discover how inaccurate it is by going back and examining the real population, and then make something squared out of it. Is that it?
-
Bonus point for finding the χ key on your keyboard.
While I'm at it.... The other thing I remember the teach banging on about forever was to do with (unlike you I haven't a clue/the will to go find symbols to type) "x-bar" [
xwith a horizontal bar on top of it] versus "mu" [the Greek letter]. x-bar was the mean you got from a sample, while mu was the actual mean, which you didn't know.Now, the problem was something about how you had to phrase what you said about x-bar & mu in your conclusion. I presume this was to do with confidence limits, you were trying to say something like "I'm 95% sure x-bar is within one standard deviation of mu". Only there was some deep rule you had to adhere to in phrasing it some way round with some wording. Like, you couldn't say x-bar or mu was likely to be whatever, because it wasn't subject to probability (perhaps that was for mu, because the mean of the population just is whatever it is, even if you don't what that is, or some-such). So what was that one all about? :)
@JonB said in Lies, Damned Lies, and Statistics:
- So that's a rather different thing from standard deviation, right. So you make a model, calculate with it, then discover how inaccurate it is by going back and examining the real population, and then make something squared out of it. Is that it?
Yep. If you say you're doing a least squares fit, then chi squared would be how good the fit was - basically the sum of the square of distances between the sampled data and the actual regression curve.
- Bonus point for finding the χ key on your keyboard.
I'm well versed in the greek alphabet, being a physicist and all. ;)
While I'm at it.... The other thing I remember the teach banging on about forever was to do with (unlike you I haven't a clue/the will to go find symbols to type) "x-bar" [
xwith a horizontal bar on top of it] versus "mu" [the Greek letter]. [...] So what was that one all about? :)In principle the real expectation value (or mean) will not coincide with the one you got by sampling. So there's some probability that the sampling mean will be in some range around the real one. That's what this is about - Student's distribution.
-
-
@JonB said in Lies, Damned Lies, and Statistics:
- So that's a rather different thing from standard deviation, right. So you make a model, calculate with it, then discover how inaccurate it is by going back and examining the real population, and then make something squared out of it. Is that it?
Yep. If you say you're doing a least squares fit, then chi squared would be how good the fit was - basically the sum of the square of distances between the sampled data and the actual regression curve.
- Bonus point for finding the χ key on your keyboard.
I'm well versed in the greek alphabet, being a physicist and all. ;)
While I'm at it.... The other thing I remember the teach banging on about forever was to do with (unlike you I haven't a clue/the will to go find symbols to type) "x-bar" [
xwith a horizontal bar on top of it] versus "mu" [the Greek letter]. [...] So what was that one all about? :)In principle the real expectation value (or mean) will not coincide with the one you got by sampling. So there's some probability that the sampling mean will be in some range around the real one. That's what this is about - Student's distribution.
@kshegunov said in Lies, Damned Lies, and Statistics:
In principle the real expectation value (or mean) will not coincide with the one you got by sampling. So there's some probability that the sampling mean will be in some range around the real one. That's what this is about - Student's distribution.
Yeah, but the nightmare recollection is something about what you were/were not allowed to "say" about something to do with the probability/confidence limits of the relationship between my & x-bar, if you phrased it wrong you lost all your marks....
BTW, on that subject there was something similar (though not as hard to remember as the mu-x-bar one) when you did "proof by induction". You did your
k, then you did yourk + 1. But when you wrote the final conclusion forninstead ofk, you had to phrase that one in a particular way too... ! -
@kshegunov said in Lies, Damned Lies, and Statistics:
In principle the real expectation value (or mean) will not coincide with the one you got by sampling. So there's some probability that the sampling mean will be in some range around the real one. That's what this is about - Student's distribution.
Yeah, but the nightmare recollection is something about what you were/were not allowed to "say" about something to do with the probability/confidence limits of the relationship between my & x-bar, if you phrased it wrong you lost all your marks....
BTW, on that subject there was something similar (though not as hard to remember as the mu-x-bar one) when you did "proof by induction". You did your
k, then you did yourk + 1. But when you wrote the final conclusion forninstead ofk, you had to phrase that one in a particular way too... !@JonB said in Lies, Damned Lies, and Statistics:
Yeah, but the nightmare recollection is something about what you were/were not allowed to "say" about something to do with the probability/confidence limits of the relationship between my & x-bar, if you phrased it wrong you lost all your marks....
Well, no idea. Formally speaking it's probably wrong to say that x bar is the expectation value (which is μ), but if using jargon you usually equate one with the other.
BTW, on that subject there was something similar (though not as hard to remember as the mu-x-bar one) when you did "proof by induction". You did your k, then you did your k + 1. But when you wrote the final conclusion for n instead of k, you had to phrase that one in a particular way too... !
Well, induction works like: "if granted for k, it is proven for k + 1, and there's some initial k for which the statement holds, then it holds for all k after the initial one" (and requires k be integer as well). I don't remember anything related to the phrasing that'd be similar to what you describe.
-
@JonB said in Lies, Damned Lies, and Statistics:
Yeah, but the nightmare recollection is something about what you were/were not allowed to "say" about something to do with the probability/confidence limits of the relationship between my & x-bar, if you phrased it wrong you lost all your marks....
Well, no idea. Formally speaking it's probably wrong to say that x bar is the expectation value (which is μ), but if using jargon you usually equate one with the other.
BTW, on that subject there was something similar (though not as hard to remember as the mu-x-bar one) when you did "proof by induction". You did your k, then you did your k + 1. But when you wrote the final conclusion for n instead of k, you had to phrase that one in a particular way too... !
Well, induction works like: "if granted for k, it is proven for k + 1, and there's some initial k for which the statement holds, then it holds for all k after the initial one" (and requires k be integer as well). I don't remember anything related to the phrasing that'd be similar to what you describe.
@kshegunov
You inspired me to Google. There obviously is a phraseology issue. I came across https://www.thestudentroom.co.uk/showthread.php?t=859544 :I don't know how you should go about concluding it; at A-level our teacher was really picky about how the wording we used to finish it (we learnt some ridiculous phrase and wrote it down at the end of every proof), but since then I haven't met anyone who really seems to care.
And there was something similar about x-bar & mu. He prolly had the same teacher as I did :)
-
Oh, shame I have not discovered this thread earlier. Cool stuff and a very pleasant read!
And to celebrate, you've all got upvotes :)
-
@kshegunov
You inspired me to Google. There obviously is a phraseology issue. I came across https://www.thestudentroom.co.uk/showthread.php?t=859544 :I don't know how you should go about concluding it; at A-level our teacher was really picky about how the wording we used to finish it (we learnt some ridiculous phrase and wrote it down at the end of every proof), but since then I haven't met anyone who really seems to care.
And there was something similar about x-bar & mu. He prolly had the same teacher as I did :)
Maybe. You might be thinking about necessary and sufficient conditions, which comes more often than not when proving math statements ...
-
@kshegunov said in Lies, Damned Lies, and Statistics:
In principle the real expectation value (or mean) will not coincide with the one you got by sampling. So there's some probability that the sampling mean will be in some range around the real one. That's what this is about - Student's distribution.
Yeah, but the nightmare recollection is something about what you were/were not allowed to "say" about something to do with the probability/confidence limits of the relationship between my & x-bar, if you phrased it wrong you lost all your marks....
BTW, on that subject there was something similar (though not as hard to remember as the mu-x-bar one) when you did "proof by induction". You did your
k, then you did yourk + 1. But when you wrote the final conclusion forninstead ofk, you had to phrase that one in a particular way too... !@JonB said in Lies, Damned Lies, and Statistics:
BTW, on that subject there was something similar (though not as hard to remember as the mu-x-bar one) when you did "proof by induction". You did your
k, then you did yourk + 1. But when you wrote the final conclusion forninstead ofk, you had to phrase that one in a particular way too... !🤔
Quod erat demonstrandum?All jokes aside,
You usually have a induction start, where you formulate your asumption:
for example:
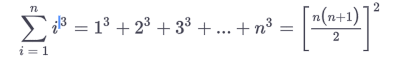
than one shows, it holds true for a specific value e.g. 1

Than the "fun" part begins when you show it doesn't matter what value you choose for example, k and k +1
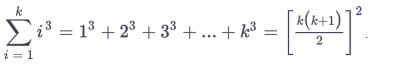
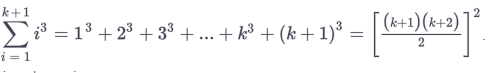
than you show that your asumptions hold true
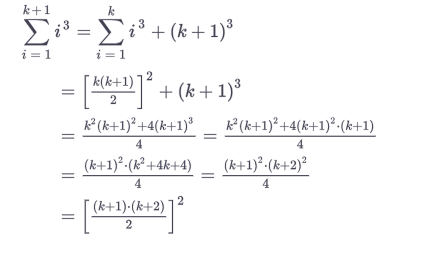
and your done, I never wrote anything else extra in my life after that.
or do you mean you had to write down the structure of the proof?
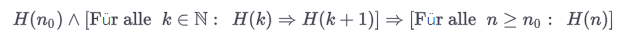
sorry for the german text: Für alle = for all = ∀ -
@JonB said in Lies, Damned Lies, and Statistics:
BTW, on that subject there was something similar (though not as hard to remember as the mu-x-bar one) when you did "proof by induction". You did your
k, then you did yourk + 1. But when you wrote the final conclusion forninstead ofk, you had to phrase that one in a particular way too... !🤔
Quod erat demonstrandum?All jokes aside,
You usually have a induction start, where you formulate your asumption:
for example:
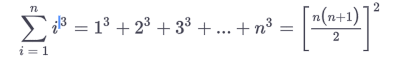
than one shows, it holds true for a specific value e.g. 1

Than the "fun" part begins when you show it doesn't matter what value you choose for example, k and k +1
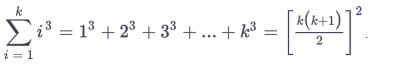
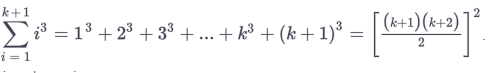
than you show that your asumptions hold true
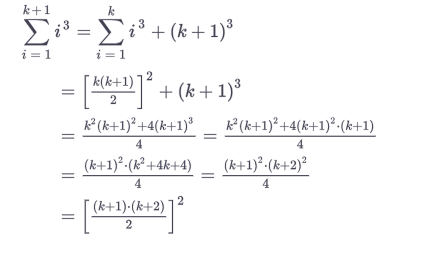
and your done, I never wrote anything else extra in my life after that.
or do you mean you had to write down the structure of the proof?
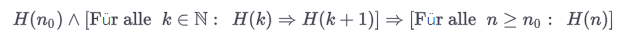
sorry for the german text: Für alle = for all = ∀@J.Hilk
That is very pretty! But, no, it was not just a question of writing QED. I refer you to the quote I pasted above, where you can see that another person has the same recollection as I have about some very specific wording we were made to use, which we have now forgotten. It was something about what we had to write for the move to generalise from1/k/k + 1ton. And something similar in the way of "special wording" when we talked about the confidence-relationship between x-bar & mu in statistics....
