Remove Duplicates from QList<CustomClass *> without disturbing its order

DonCoder

QList<CustomClass *> myList = getmylist();

Now i need to remove duplicates without disturbing its original order

possible options i know are
Option 1:

QList<CustomClass *> refinedList = myList .toSet().toList(); // But this will disturb the original order
// you may think i can sort refinedList , But i am not intersted as the comparision is a bit critical

Option 2:

QList<CustomClass *>::iterator i;
for (i = myList.begin(); i != myList.end(); ++i)
{
         if(!refinedList.contains(*i) )
         {
             refinedList.append(*i);       // This is some how o(m*n)  complexity
         }
}

I need an efficient way to do my job. Suggestions please...

[Added code tags ~kshegunov]

Christian Ehrlicher

@DonCoder said in Remove Duplicates from QList<CustomClass *> without disturbing its order:

Suggestions please...

Reverse iterate over the list and check if the item is in the list by iterating from the front. If it contains the pointer, remove it (at the position from the reverse loop)

VRonin

If you know all duplicates are next to each other: myList.erase(std::unique(myList.begin(),myList.end()),myList.end());

otherwise:

for(auto i=myList.begin(); i!=myList.end()-1;++i){
    for(auto j=i+1; j!=myList.end();){
        if(*i==*j) j=myList.erase(j);
        else ++j;
    }
}

KroMignon

@DonCoder said in Remove Duplicates from QList<CustomClass *> without disturbing its order:

I need an efficient way to do my job. Suggestions please...

My suggestion would be to use a QSet at begin, when you are building your list. And after, use QSet::toList() when you need to use it as QList

kshegunov

@DonCoder said in Remove Duplicates from QList<CustomClass *> without disturbing its order:

I need an efficient way to do my job. Suggestions please...

How large is this list? If it's under 30-40 elements the cost of the linear search is acceptable.

Otherwise, assuming memory isn't a problem, something like this.

QList<CustomClass *> current;  // Original list

QSet<CustomClass *> existing;
QList<CustomClass *> filtered;

filtered.reserve(current.size());
existing.reserve(current.size());

for (CustomClass * element : current)  {
    if (existing.contains(element))
        continue;

    existing.insert(element);
    filtered.append(element);
}

JonB

@kshegunov
Agreed. But since @KroMignon mentioned transform to QSet to get rid of dups, and that is a lot less code, would you care to comment on that in comparison to yours (because I'm interested!)? Excluding the bit I'm typing below.

@KroMignon

And after, use QSet::toList() when you need to use it as QList

For this part, the OP did specify:

Now i need to remove duplicates without disturbing its original order

I'm afraid yours fails that :( https://doc.qt.io/qt-5/qset.html#toList:

The order of the elements in the QList is undefined.

Sets are unordered, so not surprising.

kshegunov

@JonB said in Remove Duplicates from QList<CustomClass *> without disturbing its order:

Agreed. But since @KroMignon mentioned transform to QSet to get rid of dups, and that is a lot less code, would you care to comment on that in comparison to yours (because I'm interested!)? Excluding the bit I'm typing below.

Keeping the original order of items, in contrast to QSet::toList.

JonB

@kshegunov
Yes, I know that, that's not what I meant. I had in mind some comment from you about the relative efficiency of converting to QSet to achieve duplicate removal, I guess ignoring the ordering in this case?

VRonin

existing.contains(element) is pretty much constant in execution speed at the increase of the number of elements hence the speedup.

This chart (taken from here) shows this by plotting the number of lookups you can do in 1 second using different containers (QSet uses QHash internally)
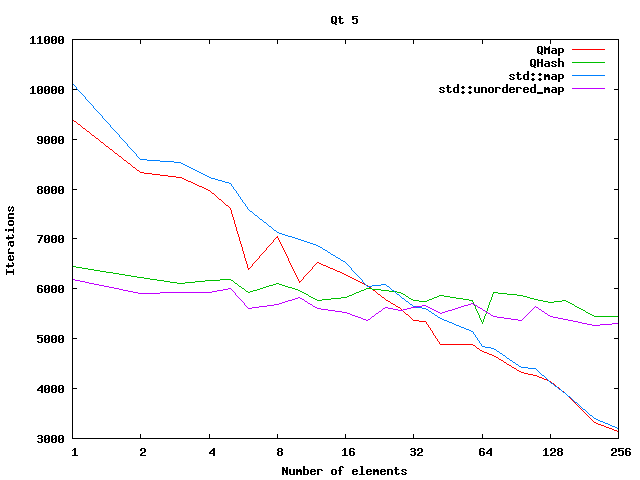
QHash vs QMap

kshegunov

@JonB said in Remove Duplicates from QList<CustomClass *> without disturbing its order:

Yes, I know that, that's not what I meant. I had in mind some comment from you about the relative efficiency of converting to QSet to achieve duplicate removal, I guess ignoring the ordering in this case?

What Luca posted. Basically:

A hash table has amortized O(1) for insertion, lookup and removal. While a vector has O(1) for insertion/removal (at the end) and at best O(log2(n)) for lookup (with binary search). Maps (i.e. QMap), which are most often implemented as red-black trees (which is also the case for QMap) have stable O(log2(n)) for said operations. As for cache friendliness vector's best, maps are worst, hash tables are in between (leaning towards maps).

The gain you have from a set (i.e. a hash table) is going to depend on two things - complexity (of the algorithm and data structure) and cache misses. You can have a vector that has filtering with O(n log2(n)) if you use binary search in the filtered vector and that's going to be fast until the vector doesn't grow too large so the linear part is going to dominate the hit you take from the hash table indirections.